秩序あるカラー配置-2

　

オストワルト表色系

■ オストワルト色立体

二重垂体

　

オストワルト表色系の空間配置（色立体）は右図のような、ソロバンの珠の形をした二重垂体です。この点で前ページと考え方は共通です。

以下、順次見てゆきましょう。

■ オストワルト表色系の色相

へリングの反対色説に基づく色相配置

オストワルトの色相は全部で24に分割されています。その基本となっているのは「へリングの反対色説」です。

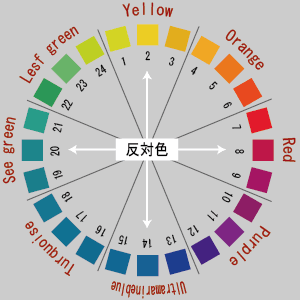
1. へリングの「心理四原色」と呼ばれる、黄―青、赤―緑の基本的な反対色対を、円周上に均等配置。
2. 次にこの中間色として、オレンジ―青緑、紫―黄緑の対を、上記配置の中間に配置 （ここまでの8色相の配置を、主要8色相と言う）
3. 主要8色相ごとにそれぞれ3等分し、全部で24の色相とする。

※結果的に前ページ「物理的配置」とほぼ同じになります。対角の色は物理補色の関係です。

色相の呼称

• 主要8色相は、黄(Yellow) 、オレンジ(Orange)、赤(Red)、紫(Purple)、青(Ultramarine Blue)、青緑(Turquose)、緑(See Green)、黄緑(Leaf Green)と呼ばれており、その頭文字をとって、Y、O、R、P、UB、T、SG、LGと表記されます。

• 上記のように、主要8色相は3分割されており、例えば黄（Y）の色相は、1Y、2Y、3Yの記号がつけられ、真ん中の2Yが代表色となっています。
  同じようにオレンジ（O）は、1O、2O、3O、赤（R）は、1R、2R、3R、.........となります。2がそれぞれの色相の代表色です。

• 色相は黄の色相1から順に、時計回りで24までの通し番号がつけられています。この番号はオストワルト色相の色相番号となります。

■ オストワルト表色系の明度

理想の白・黒、グレー

オストワルト表色系では、入射光を100％反射する色を理想の白、逆に入射光を100％吸収する色を理想の黒、その中間に有るのがグレーであると定義し、明るさの階調が心理的に等間隔に見えるよう、差をつけて配置しています。

オストワルトの明度階調

オストワルト表色系では明度階調をアルファベット小文字で表します。
ｊを除く25文字（25階調）で表記したのですが、実際はひとつおきに13文字（階調）を採用しました。
しかし実際に色表化されているのは　a、c、e、g、i、l、n、p　の8段階で、通常この8階調で明度を表します。

※ ウェーバー・フェヒナーの法則

又、明度の段階（階調）も単純に等間隔で区切るのではなく、等比級数的な変化になっています。
「刺激が等間隔で変化して感じられる為には、刺激は等比級数的に増えて行かなければならない」と言う「ウェーバー・フェヒナーの法則」を、オストワルトは明度段階に採用したのです。

オストワルト表色系の明度段階

（グレースケール図は目安）

記号	a	c	e	g	i	l	n	p
白色量（F）	89	56	35	22	14	8.9	5.6	3.5
黒色量（B）	11	44	65	78	86	91.1	94.4	96.5
グレースケール

■ 等色相三角形

二重錐体の三角形の垂直断面は「等色相三角形」と呼ばれます。
反対色（物理補色）同士、1対の等色三角形が組み合わされて菱形になります。

　

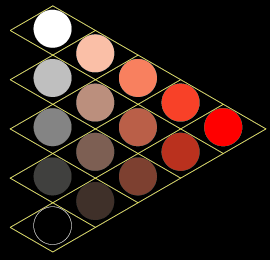
右図は　赤色相の等色相三角形ですが、どの色相でも、「純色」、「白」、「黒」を頂点とする正三角形になります。
白と黒を結ぶ底辺に、上記記載の明度段階（グレースケール）が来ます。
この明度軸を中心とした、24の色相等色相三角形配置がオストワルトの色立体、二重垂体になる訳です。

※ それにしてもこう云う図を描くときに、Illustratorのブレンド機能は便利ですね。

W+B+F=100%

オストワルトシステムでは「すべての色（物体表面色）は、白（W）、黒（B）、純色（F ）を適当な面積比で回転混色することで作られる」ということが前提となっています。
この白、黒、純色の割合を合計すると100％となる為、次の式が成り立ちます。

白（W）+黒（B）+純色（F）=100%

ただしここでの　「白」、「黒」、「純色」は現実には存在しない理想的なものです。

理想白は入射光を100％反射する色、理想黒は入射光を100％吸収する色、理想純色は或る波長を境にして、分光反射率が0％、或いは100％である色のことですが現実にはこのような色、物体表面は有りません。

理想的な「純色」を完全色（オプティマルカラー）、或いはフルカラーとも言います。
Ｆ の記号はFull Colorからきています。C （Chroma=クロマ）で表す場合もあります。

回転混色

オストワルト表色系に配置されているカラーはすべて回転混色によって作られます。
白（W）+黒（B）+純色（F）=100%　のW、B、F　を所定の割合で塗り分けた回転盤を回転させ、その継時（続）的加法混色によって得られるカラーです。

　

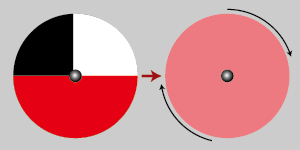
右図、左が回転前、右が回転中の模式図です。
勿論、白、黒、グレースケール、純色の作成も同じ考え方です。

理想色と現実の色

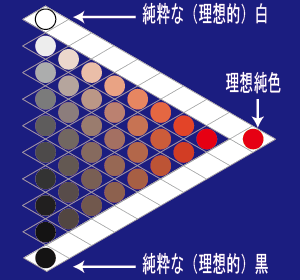
オストワルト表色系に、実際には有り得ない純粋な、理想的白、黒、純色を書き加えた図です。 右図で白い部分は理論上の理想色領域であって、現実には存在しません。

理想白は　Ｗ＝100％、
Ｂ＝0％、Ｆ＝0％

Ｆ＝100％、
理想純色は　W、B ともに0％、

理想黒は、Ｂ＝100％、
Ｗ＝0％、Ｆ＝0％

　

---

　

　

■ オストワルトの色系列

オストワルトの色票は上記のように、すべて、白量、黒量、純色量の混合比で表されています。

　

等白系列

Ｆ とＢ を結ぶ辺に平行な、すべての系列に並ぶ色票は、それぞれ同じ量のＷ を含んでいます。
これを「等白系列（isotint=アイソティント）と呼びます。

等黒系列

Ｆ とＷ を結ぶ辺に平行な、すべての系列に並ぶ色票は、それぞれ同じ量のＢ を含んでいます。
これを「等黒系列（isotone=アイソトーン）と呼びます。

等純系列

W とB を結ぶ辺に平行な、すべての系列に並ぶ色票は、純色量と白色量の混合比（オストワルト純度）がほぼ等しくなります。
これを等純系列（isochrome=アイソクローム）と呼びます。或いはシャドウ系列とも呼びます。

※ 等明度系列

色票を水平につなぐ系列は明度が等しく彩度が異なる系列。

※ この系列では色相によって成り立たない場合が有ります。次に述べます。

■ オストワルト二重垂体の矛盾

二重錐体系色立体はある程度図式的で、予め作られた枠組みに無理やり当てはめたような弱点が共通して有り、実際に我々が感覚するカラー配列からすると矛盾を生じます。
例えば上図、等明度系列に於いて、色相が赤の場合、ほぼその関係が成り立ちます。つまりグレースケール軸の明度階調と、それぞれ水平方向の色票との明度がほぼ一致します。
しかし色相によっては成り立たない場合が有ります。

明度配置の矛盾

二重垂体の中心には無彩色軸が配置されています。
この軸を含む垂直断面は、反対色同士の等色相三角形1対の組合わせでできる菱形になります。

	例えば補色同士のイエローとブルーが対になって同じ断面となり、菱形を構成します。 このイエローとブルーの等色相三角形対で、明度を比較してみましょう。 二重錐体モデルでは左右の頂点部分、つまり左図で言えば、イエローとブルーの純色が配置されている位置（つまりは純色の色相環）は、グレースケールの中央、明度の中間の位置と水平に配置されています。しかし純色同士でも実際は明度が異なります。 Y●とB● の線は本来、右下図のように明度に合わせて傾いているべきです。

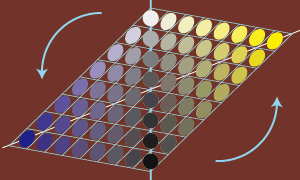彩度配置の矛盾

　

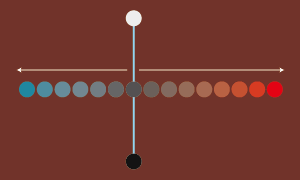二重錐体モデルでは、赤（R）とシアン（C）の純色が、グレースケール軸から水平に、等距離で配置されています。

しかし純色であっても、最高彩度が色相によって違い、●R＞C● の関係です。
本来は左図のように、無彩色軸からの距離が違うべきです。

上記補正により、感覚に合わせた色立体は、非対称、不均等なものにならざるを得ません。
これらの点を考慮した表色系として「マンセル表色系」が有ります。

---