秩序あるカラー配置-1

物理的特性に基づく色彩の空間配置

■ 表色系

三属性

色彩を、物理的特性や人間の感覚など、ある基準に基づき秩序立てて配置したものを「表色系」と言います。配置する基準によって、幾つかの表色系が考えられています。 通常、「色彩の三属性」と呼ばれる、色相（Ｈｕｅ）、明度（Ｖａｌｕｅ又はBrightness）、彩度（Ｃhroma又はSaturation）が配列の基準となります。

色立体

基準が三つあることで、その配列は自然に三次元、つまり立体的な空間配置にならざるを得ません。これを「色立体」と言います。
オストワルト表色系、マンセル表色系などが有名ですが、このほかにも幾つかの表色系が存在します。
表色系が多数存在すること自体、全ての基準を同時に満たす、唯一のカラー配列システムは無い、と言うことの表明でも有ります。

ここでは先ず、物理的特性に基づく配列を見てゆくことで、その考え方を理解し、次にオストワルト表色系とマンセル表色系について、その違いと共通性について述べてみたいと思います。

■ 純色の配置（色相環）

減法原色と加法原色の配置

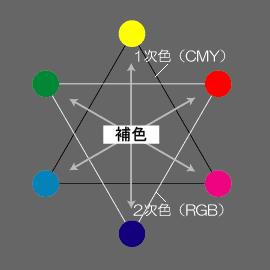
最初に色相を配置してゆきます。色相はスペクトルにおける波長（周波数）の違いが基礎になります。
波長は本来、長から短へ（低周波から高周波）への直線的な変化です。従ってスペクトルも当然直線状の配列になります。
ここにスペクトルに無いマゼンタを加えることで、長波長域（赤系）と短波長域（青系）を連結し、円周上に配置することが出来ます（「スペクトルに無い色、マゼンタ」参照。
これを「色相環」と言います。

1. 最初に純色を配置してゆきます。
   先ず基本色（一次色）としての減法原色-CMY-を、等間隔で配置します。
2. 次に副次色（二次色）としての加法原色-RGB-を、1との対極に配置します。
   このとき向かい合った一対の色は、補色の関係になります。

中間純色の追加

3. 上記6色の間に、中間色を挿入・配置します。 これにより12色となり、さらにこれを繰り返して行きます。

原理的にはほぼ限りなく細かく配置できる訳ですが、人間の目が識別可能な純色はおよそ300色と言われており、それ以上の細分化は意味が無いことになります。

配置されたカラーは順序をたどり、又、元に戻ります。つまりカラーの配列は円形になり、始まり・終わりが有りません。
これを、色相環と言い、円周上に配置された角度による、色相の違いを表します。
そして色相環の際外周には、その色相の中で最も彩度の高い色（最もその色らしい色）が配置されることになります。

■ 無彩色の配置（明度の基準）

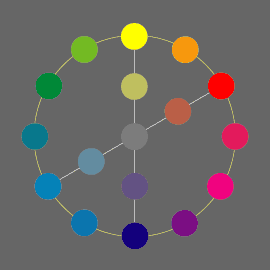4. 次に無彩色を配置します。

対角位置の2色は補色の関係になっています。つまりその2色の色材を混ぜ合わせると、減法混色により中和して灰色（無彩色）になります。
従って色相環の中央には必然的に純色同士の混合である無彩色が配置されることになります。

無彩色とは色相及び彩度を持たない色、つまり全く明るさを含まない状態（黒）と明るさの飽和状態（それ以上明るさを増やすことが出来ない状態―白）、及びその中間の様々なレベルの灰色のことです。色相の影響を全く受けない中性的な色であり、明るさの違い(明度）だけで区別します。

グレースケール

左図は黒から白までを、人間の目での識別範囲とされる150階調で示したものです。
（拡大図で階調ごとの明度差が分かりますか）。

無彩色の秩序有る配列は、白→黒、或いは黒→白の一方通行で、図のように直線的な配列になります。グレースケールとも言います。

このグレースケールが色相環の中央に、色相環と直角に配置されます。
この配列が、明度の基準になります。 直線的距離は、明度の差になります。

■ 純色と無彩色との距離（彩度の基準）

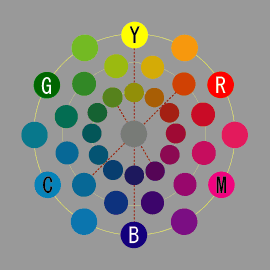
純色と無彩色

色相環の最外周に純色が、中央に灰色が配置されています。
純色と灰色との間にその混合色が配置されます。
色相環の最外周は最も彩度が高く、中央に行くに従い彩度が低くなり、中心には全く彩度のない無彩色（グレースケール）が配置されることになります。

中心を基準として、全ての対角に有る色同士の混合は、中央の無彩色（灰色）となります。

■ 無彩色と純色との配置

色立体

無彩色の配置（グレースケール）も、純色の配置（色相環）もそれぞれは、１次元(直線）或いは2次元（平面的）な配置です。
これを統一して一つの配列にするには、3次元的な配置が必要になります。
このような考えで作られたカラーの配置を「色立体」等と言います。

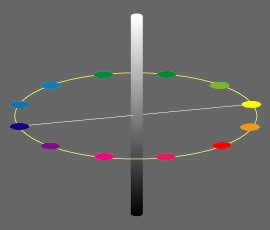5. 中央に無彩色の配列が来ます。
   色立体では常に白を上、黒を下に配置する決まりが有ります。
6. 無彩色の配列の周りに、色相環が来ます。
7. 無彩色と色相環の組み合わせが、この色立体の骨格になります。

色相環の純色と、無彩色上部の白、下部の黒を結ぶ線上に、それぞれの純色と、白・黒の混合で作られる、様々な明澄段階が配置されます。

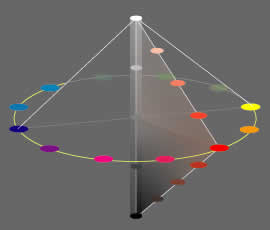
8. 白に近づくにつれ、明度が上がり、彩度が下がります。
9. 黒に近づくにつれ、明度が下がり、彩度も下がります。
10. 二重錐体
    右図で、全ての純色と白・黒を結んだとき、算盤の珠のような形、二重錐体となります。

※ 「物理的特性に基づく表色系」と、オストワルト表色系

ここで述べた「物理的表色系」は、考え方として次に述べる「オストワルト表色系」と多くの共通性が有ります。 ...と言うよりも実際世上に流布しているのは、オストワルト表色系です。「物理的表色系」はその理解の為の考え方を述べたものです。

二重垂体についても、次ページ「オストワルト表色系」で取り上げます。