加法混色とRGB

　

加法原色と加法混色

■加法三原色

スペクトルと加法三原色

「スペクトルとカラー」の復習になりますが、連続的に変化するスペクトルの、それぞれ1/3ずつの領域をまとめると、波長の長い順から、赤（Red）、緑（Green）、青（菫青-Blue）が得られます。

これを「加法三原色」、或いは「光の三原色」と言い、それぞれのイニシャルを取って、一般的にはRGBカラー、或いは単にRGBと呼びます。
加法三原色は加法混色の素材となります。

• 波長の長い方1/3は、R（赤）
• 中間1/3は、G（緑）
• 短い方1/3は、B（青）

■加法混色

三原色光の混合

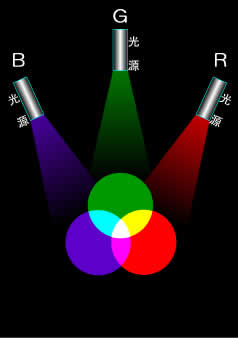
加法三原色の色光（R・G・Ｂ）を、適切な割合で再混合することによって、スペクトルに含まれるあらゆる色光を再現することが出来ます。
元々、加法三原色-RGB自体、スペクトルの構成成分である以上当然とも言えます。 RGB全ての混合は、太陽光線と同じく白色光になります。

加法混色は、直接、光を混ぜ合わせることでカラーを作るシステムです。舞台照明やカラーTV、コンピュータのモニタ画面表示等に関わる現象です。

加法混色の考え方

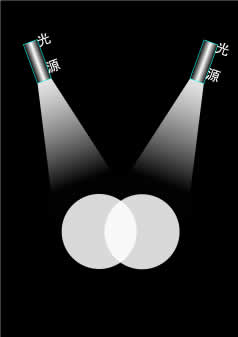
加法混色の理解は比較的容易だと思います。
懐中電灯1個で照らすより、2個、3個と照明を増やすことで明るさが増しますが、イメージとしては同じことです(右図）。
照明の量が少ないうちは、その量を増やすごとに明るさも増して行きますが、ある程度になると、それ以上に照明を増やしても明るさは変わらない状況になります。 つまり飽和状態になった訳です。

加法混色でも、三原色光の混合によって出来る色は、原色より常に明るくなり、三原色それぞれ最高輝度の混色は飽和状態の白になります（右上図）。

■加法混色の種類

加法混色には次の三種類が有ります。

同時的加法混色

加法混色の基本的な方式です。

右図のように、光が重なっている場合です。舞台照明、カクテル光線など。

CG等、コンピュータのカラーシステムでは、R・G・B それぞれを256階調に分けることで、その組み合わせとして256の3乗、つまり16,777,216万色を表現できるようになっています。

なおカクテル光線一個一個の光源は、通常カラーフィルタで色光を作っています。 このこと自体は「減法混色」です。
今は光そのものに色がついているLEDが開発されて、フィルタを必要としなくなっているかも知れません。

併置的加法混色

非常に近い位置で隣り合っているカラーを見た場合、それらが一緒になって一つのカラーに見えます。 例えば、点描絵画、色の違う縦糸と横糸で折られた布の色等。

カラーTV・モニタ等も併置的加法混色です。
カラーモニタは、RGB3色にそれぞれ感応する蛍光体が並んでおり、そこに電子銃からのビームを走査させて発光させます。
我々は、ごく近い位置に並んだRGB三色を同時に見ることにより、その組み合わせで様々なカラーを感じます。
又、インクジェットカラープリンタ等も、次ページで説明する「減法混色」と合わせ、「併置的加法混色」を使い、様々なカラーを作り出しています。

継時（続）的加法混色

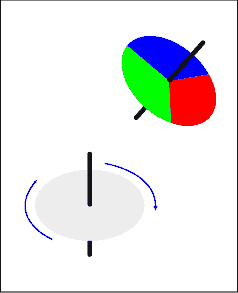
違うカラーを連続的に見た時、交じり合って一つのカラーに見えます。
回転面に別々なカラーを配したコマを廻した時、カラーが交じり合って中間のカラーが出現すると言う様な場合です。

※ 同時的加法混色と他の加法混色の違い

上記カクテル光線の例では、光による混色で完全な加法混色と言えます。カラーの追加が明るさの上昇に繋がります。
しかし他の、併置的加法混色と、継時的加法混色の例は、別なカラーを追加するとその分他のカラーの配分が減り、従って明るさが増す、と言うことは有りません。
そのためこの二つの方式を「中間的加法混色」等とも言います。

ただし、併置的加法混色で有っても、カラーモニタは完全な加法混色と言えるかも知れません。つまり電子銃ビームの量を自由に調整することで、個々のピクセル（画素）の輝度を調整できるからです。ピクセル個々の輝度が変われば、画面全体の輝度も当然変化します。

---

　

■加法混色の体系化（グラスマンの法則）

限られた加法三原色の混合だけで、あらゆる色を作り出せると言う、加法混色についての基本原理を実証し、体系化したものとして、「グラスマンの法則」（1853年）があります。
これは後に、CIE XYZ表色系の基礎ともなり、現在に応用されています

※ 等色実験

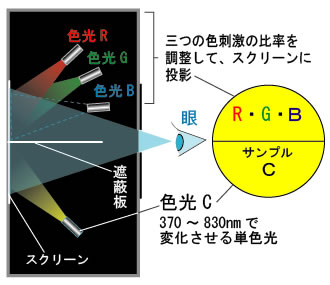
グラスマンの法則を知る前に、等色実験について理解しておく必要が有ります。
右図のように、用意された色光の組み合わせや強さを調整して、サンプル光と同じ色にすることを「等色」と言います。

1. 遮蔽版で仕切られた下のスクリーンに様々な単色光を照射。
2. 上のスクリーンには、R,G,Bの三色光（原刺激と言います）の量を、それぞれ適当に調整して混合照射。
   双方を目視で比較する。
3. 単色光 C に、どんな色を持ってきても、RGBだけの適切な混合によって全く同じ色を作り出せることが分かっている（...と思われていた）。

※ 三原色で等色出来ない色、スペクトルに無いのに等色出来る色

しかし実際の等色実験では、三原色光をどのように混合しても等色できない、つまり作り出せないスペクトルの色が有ることが分かりました。
具体的には、550nmより波長の短い緑色や青色のスペクトルの色は、ＧとＢの混合で等色ができる筈なのだが、実際にはどんなに混合割合を変えてみても、等色することが不可能だと云うことです。
逆にスペクトルにない光の色、例えば赤紫色（マゼンタ）はスペクトルに無い色だが、ＲとＢの混合で作ることができます。

つまり、感覚で捉えられる三原色と、光学原理で考えられる三原色がイコールでは無かったと云うことが分かり、人間の受光感覚に適合する三原色を使って、スペクトルの色を等色しようという作業が行われました。
新しい三原色は、ＲＧＢを相互に足し合わせ、もとのＲＧＢを修正することにより、作り合わされました。
これによって作り出された色は、スペクトルに実在する色ではありません。
したがって、ＲＧＢの代わりに、ＸＹＺという三記号を使うこととし、三刺激値と呼ぶことにしました。
このような三刺激値の加法混合で、スペクトルの色もスペクトル光の混合色も、物体の色もすべて表色することに成功しました。

この発展形があの、馬蹄形ともヨットの帆の形とも言われる、CIEのxy色度図に結びついているのでしょう。

1、色の三色性（グラスマンの第一法則）

加法三原色（R・G・B）の色刺激による加法混色によって、あらゆる色を作り出せる。
実は等色する色刺激は、独立した色つまり、どの1色も残りの2色の加法混色で作ることが出来ない色で有れば、必ずしもＲ、Ｇ、Ｂ に限らないが、通常はこの三色が使われる。

条件等色（メタメリズム）
ここで重要なことは、サンプル色光 C が、どのような波長によって構成された色かを問わず、R,G,Bの三刺激値によって「等色」されると言うことです。
550nm（緑）と650nm（赤）の波長を混合した光は、人間にとって黄色に感じられます。
或いは長波長域2/3のスペクトルを集めても黄色として感じます。
しかし又、 元々スペクトルには、600nm波長に単色光としての黄色があります。

つまり物理的には全く違う波長構成を持った光であっても、人間にとって「同じ色」だと感覚されるケースはいくらでも有り得ます。 波長構成がどのようであるかに関わらず、人間にとって同じに見えるサンプル色光 C は、全て、R,G,Bの同じ混合比で等色することができます。
これを条件等色（メタメリズム）と言います。

もう一つ重要なことは、サンプルCと等色する、R,G,Bの混合組み合わせは1種類しかない、と言うこと。 つまり原刺激を、R,G,Bと決めておけば、サンプルCの値は一義的に特定出来ます。

2、色の連続性（グラスマンの第二法則

加法混色に用いる三つの色刺激のうちの、一つの混色量を連続的に変化させると、混色によって作られる色も連続変化する。

3、色の等価性と加法性（グラスマンの第三法）

色の等価性
等色している色光は、その波長構成がどのようなものであっても、加法混色において同じ効果をもたらす。 つまり、見え方が同じ色であれば、それがどのような波長構成の光であっても、加法混色に用いた結果は同じになる。

色の加法性

色の等価性から、色の加法性を導くことが出来る 。
上図「等色実験」において、サンプル色光Cに、別のサンプル色光C'を加えて出来た色光C-2は、色光Cと等色した原刺激R・G・Bに、色光C'と等色した原刺激R'・G'・B' を加えた原刺激-2と等色が成立する。

　

視覚系と加法混色

■ 視細胞のカラー認識

人間の眼が色彩を感知するシステムは加法混色です。
......と言うより、人間にそのシステムが備わっているからこそ、R・G・B 三色の混合であらゆるカラーを作り出せると言う現象が成り立つのでしょう。

条件等色（メタメリズム）からも分かるように、上記「グラスマンの法則」で表される、加法混色の法則性は、人間の眼が色を認識するシステムに基づいています。 つまり人間は物理的な光の組成ではなく、網膜上の3つの錐体への刺激をもとに色を感じているのです。

グラスマンの法則と錐体

人間の眼の網膜には、錐体と杆体という二種類の視細胞が並んでおり、色の認識は錐体が担っています。
人間の錐体は三種類あり、それぞれ長波長域、中波長域、短波長域の光に感応しています。 そしてその波長構成の違いを、この三種類の錐体への刺激として捉え、脳の中で色の感覚を作り出しています。

光に含まれる波長の構成により、三種類の錐体への刺激の割合が変化し、色の感覚信号となります。 このとき、三錐体への刺激が同じであれば、光の波長構成は違っても、眼は同じ色だと感覚するのです。
つまり物理現象としての光の波長特性を、必ずしも忠実に反映している訳では有りません。

「光とカラー」で述べたように、色の違いは電磁波波長の違いです。波長によって色は一意的に決定されます。つまり波長が同じなら色も又同じです。これは単一色、或いは単色光と言います。
しかし逆は必ずしも真ではありません。人間の目には、全く異なった波長であってもその組み合わせで別の波長色と同じに見えるケースは幾らでも有り得ます。これが混色で有り合成色です。

例えば、600nmにピークを持つ1つの光と、550nm及び650nmピークを持つ2つの光との2つのケースが有った場合、各錐体が受ける刺激の比率は、どちらも同じと言うことが有り得ます。 錐体が受ける刺激の比率が同じ場合 、眼はこの2ケースの光の「色」を区別することが出来ず、どちらも同じ色、この場合では「黄色」と判断します。

ドの音（C）とミの音（E）の2つの音を同時に聞いたとして、人間の耳は2つの音として聞き分けます。混合して一つの中間のレ（D）の音として聞こえる訳では有りません。
しかし視覚は、同時或いは極めて近い位置で複数のカラーを見た場合、網膜の錐体刺激が結果的に同じレベルになるならば、その波長構成を問わず、混合された一つの同じ色として見ると言うことです。耳に比べて目の、この一種曖昧さが混色の前提となっているんでしょうね。

このように三つの錐体が受ける刺激の比率によって、様々な「色」を合成して感じる訳ですが、その刺激は上記の様に、錐体の感度ピークに一致している必要は無く、特にどの波長の光でなければならない、と言うことも有りません。
スペクトルの二つの色の混合がスペクトルの他の色と同じ色になる。このような光の成分が違いながら、人間の目には同じ色に見える現象をメタメリック・マッチング、略してメタメリズムと言います。

色は物理的な存在であるとともに、人間の感覚を通して認識される存在でもある訳です。

錐体

錐体は色の違いを識別し視力も良いのですが、錐体が機能するためには多量の光刺激が必要で、暗いところでは機能しません。 つまり、暗いところでは色を感じることが出来ず、次に述べる杆体の機能である明暗の違いだけが感覚されます。

杆体

杆体は一種類だけです。 従って光の波長構成の違いを区別することが出来ず、色の感覚を持つことが出来ません。 光の強度、つまり明暗の違いだけを識別します。

スペクトルの全領域に反応しますがピーク波長は約510nm。
光に対する感受性はきわめて高く、光子1個に対しても感応するそうです。 逆に昼間や明るい照明の元では、大量の光で飽和状態となり機能せず、錐体だけが機能しています。
杆体は専ら、暗いところでの視力を担っています。

※視細胞の分光分布

実線は錐体です。錐体は三種類あります。
点線は杆体の感度曲線です。ピークは510nm。

S錐体、又は青錐体（B錐体）

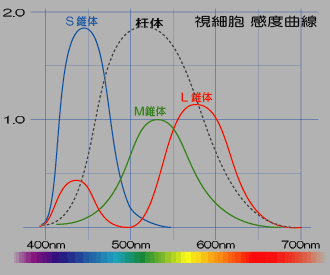
短波長域、400～500nmに感受性を示し、ピークは430nm。

M錐体、又は緑錐体（G錐体）

中波長域、500～600nmに感受性を示し、ピークは530nm。

L錐体、又は赤錐体（R錐体）

長波長域、550～650nmに感受性を示し、ピークは560nm。
赤錐体のピークは必ずしもRed域では有りません、どちらかと言うと、黄緑から黄色域です。

■ 可視光線波長域の根拠

ではなぜ人間は、幅広い電磁波の波長域の中で、上記波長域にのみ感度を示し、「可視光線」となっているのでしょうか。

1. 太陽光線の波長分布
   地上における日中の太陽光線の中で、もっとも強い波長領域がこの、760～380ナノメータ近辺です。
   人間を含む殆ど全ての生物が、種によって多少のぶれは有るにしても、この領域の電磁波に感度を示し、太陽光線のエネルギーを最大限に利用することに特化する形で進化してきたからでしょう。
2. 分解能
   もうひとつの理由として分解能の問題が有ります。
   実は「波長」の長さはものを見分ける「分解能」と直接関係して来ます。その波長よりも小さいものは見分けることが出来ないのです。
   光学顕微鏡では、可視光線の波長の制約で、どうしても1000倍程度にしか倍率を上げられず、それより小さいサンプルはさらに波長の短い電子顕微鏡を使うしかないのもそう言う理由です。
   
   人間を含む全ての動物は、自分の体の大きさを基準にして、餌や敵を識別できる程度の波長域の電磁波に感度を示すよう、長い進化の過程で淘汰圧が掛かって来たのでしょう。

---