サイト内用語検索
クリックしてウインドウを開き、必要に応じてウインドウ幅を調節して閲覧してください。
光とカラー
カラーの基礎は光です。光、特にスペクトルとの関係抜きにカラーの理解は出来ません。同時に光（電磁波）は物理現象のコア概念であり、20世紀物理学の発展は、相対性理論にしても量子論にしても、光・エネルギーの研究がその発端となったと言えます。
その意味で、光とカラーは、人類の物質理解の最先端部分だと言えるかも知れません。
電磁波
■ 電磁波と可視光線
光は「粒子（光子）」と「波（電磁波）」の両方の性質を持っていることが、現在分かっています。「光とカラー」を理解する上で、特に「波」の性質に着目して考えてみることにします。
周波数による区分
われわれが通常「光」と呼んでいる可視光線は、電磁波の一種です。一種と言うより、周波数・波長の違いによって性格の異なる電磁波の、ある領域（波長域）を差す概念です。
電磁波を一言で説明すると、「電気と磁気が相互に作用して発生するエネルギーの波」と言うことになります。つまり光とはエネルギーそのものと言えるでしょう。
周波数と波長の関係
「電磁波（光）」の中身に入る前に、周波数と波長の関係について、復習も兼ねてふれて置きます。
なお周波数とエネルギーの関係には、電磁波（光）特有の事情も有ります（直ぐ下、「振幅・周波数とエネルギー」参照）。
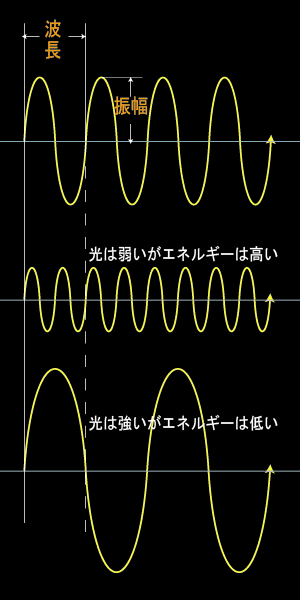
- 周波数
1秒間における波の数を「周波数」と言います。
電磁波の周波数は、その電磁波のエネルギーに比例します。 - 波長
1サイクルの波の長さを「波長」と言います。 波長と周波数は逆比例します。 - 振幅
波の高さを「振幅」と言います。
振幅は電磁波の強さに比例します。光で言えばその明るさに比例します。
波長が短い程周波数が高くなり、エネルギーが高くなります。振幅が大きいほど光が強くなります。しかし、電磁波の場合振幅の大きさはエネルギーの大きさに繋がりません。（※ 下記参照）
※振幅・周波数とエネルギー
紫外線は周波数が高く、仮に曇って弱い紫外線（振幅が小さい）でも日焼けを起こし、長く曝されるとDNAに損傷を来たします。つまり化学的なエネルギーが高い。
それに対し周波数の低い赤外線は幾ら強くても日焼けを起こすことは有りません。
強い赤外線（振幅が大きい）は火傷を起こすが、これは「熱線」とも呼ばれる赤外線の物理的作用。
振幅の大きさ（光の強さ）が、エネルギーの高さに繋がらない、と言うことは非常に奇異な話です。
例えば水の波で言えば、振幅（波の高さ）が高い程、津波のエネルギー・破壊力が高いことは普通に理解できることです。 しかし「光」については事情が異なります。
これは光が電磁波として「波」の性質を持つと共に「光子」として粒子の性質も持っていることによります。
その辺の事情を定式化したのが、アインシュタインの「光量子説」理論です。アインシュタインがノーベル賞を受賞したのは「相対性理論」に対してではなく、この「光量子説」に対してです。
可視光線
電磁波は周波数が低い（波長が長い）方から順に、電波、赤外線、可視光線、紫外線、エックス線、ガンマ線に分類されます。つまりこれらは皆、素性は同じだと言えます。周波数・波長の違いだけですが、しかしその違いによってそれぞれの電磁波の性格は全く異なります（下図参照）。
その幅広い周波数帯の、ホンの僅かな帯域、およそ760ナノメータから380ナノメータの波長域に対し、人間の眼は感受性を示します。つまり可視光線として認識します。カラーとの関係で専ら問題になるのは、当然この可視光線です。
可視光線の外側には、赤外線（長波長域側）と紫外線（短波長域側）が続いています。
「光」と言った時、普通は可視光線を差すのですが今では、赤外線も紫外線も光として扱うケースが多いようです。赤外線カメラ、或いはブラックライトのように、何らかの装置を介して赤外線も紫外線も「可視」できるようになってきたと言う事情が有るのでしょうね。
我々に（多分）今一番なじみの深い照明システムである蛍光灯も、その発光原理の基礎は紫外線です。
スペクトル
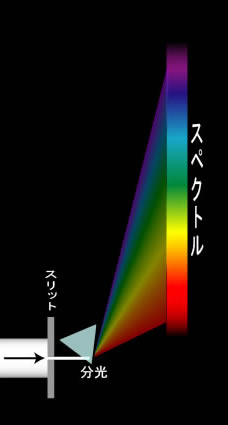
太陽光（白色光）をプリズムに通すと虹のような連続した色の帯が現れます。
太陽光には周波数の異なる様々な光成分が含まれており、通常それらは交じり合って白色光（無色）として感じられます。
周波数の違いは、光の屈折率の違いとして現れますから、混合色としての白色光をプリズムに通すと、周波数の違いによって屈折・分光され、単色光の連続的な帯になる訳です。
この現象を発見したのはニュートン（1668年）ですが、ニュートンはこの色の帯を「スペクトル」と名づけました。
一般に「スペクトル」とは光の成分を、波長の順にならべたもののことを言います。狭い範囲の可視光領域（およそ、760nm～380nm）にもこのような連続的な波長変化が見られると言うことです。
ニュートンが発見したのは可視光スペクトルであり、カラーとの関係で問題になるのもこの可視光スペクトルですが、対象とする波長域の違いによって、それぞれ赤外スペクトル、紫外スペクトル、X線スペクトルなどが有ります。
※ 下のスペクトル図は、説明のため便宜的に描いたもので、正確な色では有りません。モニタの状況によっても変わってきます 。 この事情は以下の全ての図において、同じです。
|
■ スペクトルとカラー
波長ごとに分光されたスペクトルの、特定領域を再混合することによって、任意の色光が得られます。
加法混色の基礎となる考え方です。
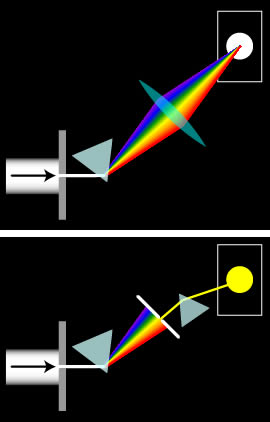
スペクトルの再混合
白色光はプリズムによって、スペクトル成分に分解されます（分光）。
分解されたスペクトルをレンズで再度収束すると、混合されて白色光の焦点スポットになります（右図）。
単色光
単一の波長のみを含有している光を単色光（モノクローム）と言います。
単色光はこれ以上分光できない色光の最小単位です。 単色光を日常的に見ることは有りません。
スペクトルに分解された光は、その波長成分ごとに取り扱いが可能となります。
特定の波長域だけを選択的に取得した場合、その波長に応じた単色光が得られます。
単色光をさらに次のプリズムに通しても、それ以上には分離されない。つまり単色光を分光することはできません（右図）。
単色光はその名の通り、単一の波長しか含まれておらず、分光する要素がないからです。
連続スペクトルと線スペクトル
太陽光や白熱灯の光は虹のような連続スペクトルになります。これはその光の源が「熱放射」で有ることに拠ります。光源の温度（例えば太陽表面の温度、6000度）に対応した連続スペクトルが発生します。
一方、高速道路トンネルのナトリウム灯スペクトルは、黄色一色の線形のスペクトルしか出て来ません。
これはナトリウム光が単一の波長しか含んでいない為です。つまりナトリウム光は単色光です。 このようなスペクトルを線スペクトルと言います。
水銀灯のスペクトルは複数の線スペクトルになります。
一般に気体原子の発光は、その原子特有の線スペクトルとなります。それはその発光が熱放射ではなく、原子がエネルギーをやり取りする際の「電子遷移」と呼ばれる現象に拠るからです。線スペクトルを調べることで発生源の元素を特定することができます。例えば遠い宇宙の星の物質分布等を特定することができます。
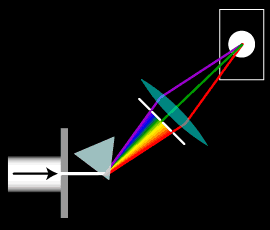
単色光の再混合
スペクトルの再混合によって、白色光が得られることは上記で見ましたが、適切に選択された単色光の組み合わせによっても、白色光が得られます。
例えば、短波長435nm（青―菫色）中波長546nm（緑）長波長700nm（赤） の単色光を混合しても白が生じます。
この三色光の強度をそれぞれに変化させることによって、白だけでなく全てのカラーを作ることが出来ます。 これが「加法混色」の基礎です。
スペクトルと７色
スペクトルが７色である、と最初に言ったのもニュートンだそうです。その影響も有ってか、虹も７色と言うことになっています。
しかし、これには科学的な根拠は有りません。 人間にとって何色に見えるか、或いは何色に見たいか、と言う意味合いから決まったことでしょう。
ラッキーセブン等と言って、ヨーロッパでは 7 は特別な数のようです。
音階が7度で循環していることからも来ているのでしょう。カラーも「赤」「橙」「黄」「緑」「青」「藍」「紫」と経過して、又赤に戻り、循環します。（※ 色相冠）
国や民族によって、虹の色を6色或いは2色としているケースも有るそうです。
原色、補色、混色
■三原色
原色とは 「他の色との混合で作り出すことの出来ない色」のことです。
その原理的基礎はやはりスペクトルを中心とする物理的な現象です。 或いは人間の眼が色を感ずる生理機能から来ています。
コンピュータグラフィックに限らず、絵画、染色等、カラーシステムを考えるうえで重要になってくるのは、加法三原色と減法三原色です。
補色とは「合わせて白になる関係の色」或いは「白から、或る色を取り除いたときに残る色の関係」のことです。 加法三原色と減法三原色は、補色の関係になっています。
加法三原色
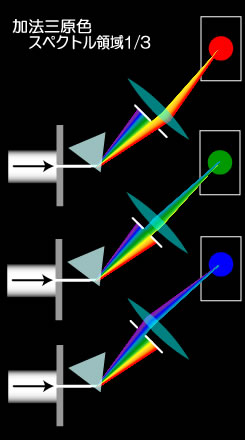
可視光スペクトル領域の、長波長域1/3だけを混合すると「赤＝Red」が得られます。
同じように中間域1/3だけの混合で「緑＝Green」が、 短波長域1/3だけの混合で「青（青紫）＝Blue」が得られます。
これを「光の三原色」或いは「加法三原色」等と言い、色の名前をそのまま並べ「RGBカラー」とも言います。
加法三原色は舞台照明やカラーモニタなど、色光の配合、つまり加法混色の際に元となる色光です。
この三色の光を混ぜ合わせると、白色になります。
減法三原色
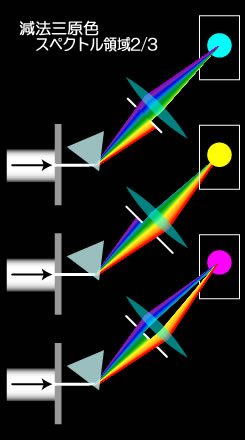
可視光スペクトル領域の、短波長域2/3を混合すると「シアン青＝Cyaan」が得られます。
同じように長波長域2/3の混合で「黄色＝Yellow」が、得られます。
そして、短波長域1/3と長波長域1/3（合計2/3）の混合で「マゼンタ＝Magenta」が得られます。 なお、マゼンタだけはスペクトルに含まれていない色です。
これを「色の三原色」或いは「減法三原色」等と言い、色の名前をそのまま並べ「CMYカラー」、或いはブラックを加えて「CMYKカラー」とも言います。
減法三原色は絵の具や、印刷インキなどの配合、つまり減法混色の際に元となる色です。
この三色のインキ、絵の具を混ぜ合わせると、黒色になります。
補色
加法原色はスペクトル領域の1/3、減法原色は2/3 を含んでいて、合わせるとスペクトルの全領域をカバーすることが分かります。
スペクトル全領域の混合は白色光になります。つまり、RとC、GとM、BとY は、それぞれの組み合わせで「白」になります。
このように、「合わせて白になる関係の色を補色」と言います。逆の言い方をすれば「白から、或る色を取り除いたときに残る色」との関係とも言えます。
加法原色と減法原色は、補色の関係です。
■ スペクトル、三原色、補色の関係
「加法三原色」「減法三原色」「補色」の関係をまとめると下図のようになります。
そしてこれらの関係が、全てスペクトルに基礎を置いた、つまりは物理的な現象であることが理解できます。
スペクトル
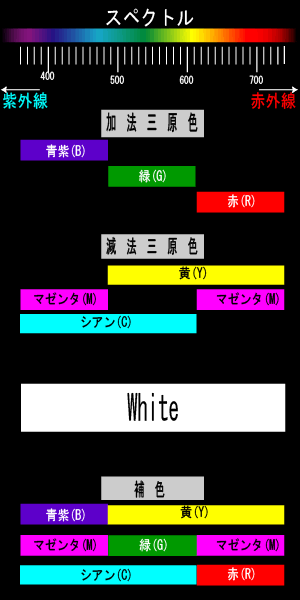
波長の短いほうから、紫、藍、青、緑、黄、橙、赤と無段階に推移する。 「赤」は680nm位から色が変化しない。
短波長域は紫外線に、長波長領域は赤外線に繋がり可視領域から外れる
加法三原色
スペクトルの3分の1ずつの領域をまとめると加法三原色（RGB）が得られる。
減法三原色
スペクトルの３分の2ずつの領域をまとめると 減法三原色（CMY）が得られる
混色
スペクトルを全て混合すると、白色が得られる。
補色
足して白色になる対の色を「補色」と言う。 或いは白から或る色を取り除いたとき、残った色との関係。RGBとＣＭＹが補色関係になっていることが分かります。
※ 上記に関し付け加えると、加法三原色RGBは、スペクトルのそれぞれ1/3づつなのに対し、減法三原色CMYは、スペクトルの2/3を含んでいます。
つまり、色光そのものはCMYの方がRGBよりも明るいのです
■原色の混合
上記、原色・補色の関係を「混色」によって確認してみましょう。
混色（加法混色、減法混色）は、「光とカラー」のいわば中心テーマみたいなもので、次ページ以降で詳述しますが、ここでは簡単に双方の関係について見てみます。
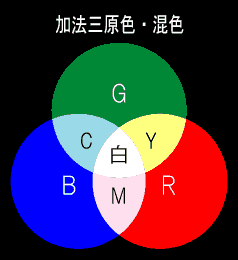
加法三原色
R・G・B はスペクトル領域の、それぞれ1/3づつですから、2色の混合で減法原色 C・M・Y （2/3)が生じます。
三色全ての混合で3/3となり、飽和して白色となります。
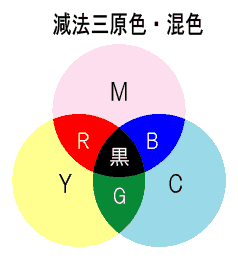減法原色と混色
減法三原色 C・M・Y はスペクトル領域の、それぞれ2/3です。
従ってその補色は1/3と言うことになります。
減法混色は絵の具やインキ等、色材の混合で考慮される問題です。
例えばマゼンタ＝Magenta と、シアン＝Cyaan の絵の具を混合すると、それぞれ1/3づつの補色光が吸収され、残りのBlue が残ります。
三原色と補色
上図を比較すると分かりますが、加法三原色と減法三原色は、重ねるとピッタリ補色の関係になっていることが分かります。
※ 原色とは「他の色を混合することで作り出すことの出来ない色」のことですが、 上図を見ると、加法原色の混合で減法原色を、減法原色の混合で加法原色が出来ています。
「他の色との混合で、原色が作られているじゃないか」と仰る向きも有るかも知れません。
確かに、R・G・B の光の混合で C・M・Y の色光を作ることが出来るし、C・M・Y のインキの混合で R・G・Bの色を作り出すことが出来ます。
しかし、これは問題が違います。
RGBによる「加法混色」と、CMYによる「減法混色」は、そのシステムが全く違う、と言うか逆です。
加法混色で、加法原色を作り出すことは出来ないし、減法混色で減法原色を作り出すことは出来ません。
それぞれの「原色」は、やはり「他の色を混合することで作り出すことの出来ない色」です。