Illustrator基礎講座 -デジタル2
HOME > 基礎講座 > デジタル > 2進数とビット > NEXT

サイト内用語検索

クリックしてウインドウを開き、必要に応じてウインドウ幅を調節して閲覧してください。

Movable type-ベースにページを切り替えました

新しいページはこちらをご覧下さい。或いはHOMEから入って下さい
現在表示のページは、低解像度（狭い）モニタ用に残して有ります

　

「ビット」！！、
コンピュータを含め、あらゆるデジタル機器、通信、ソフトウエアの全ての領域にわたって顔を出す最も基本的な概念。情報の最小単位。そしてその基礎となっている2進数。
ビットの理解と2進数に慣れておくことは、パソコンを自覚的に使いこなす上で必須でしょう。勿論illustratorを使いこなす上でも。

Illustrator講座、PC音痴駆け込み寺-共有

2進数

前項「デジタル」の、コンピュータへの具体化がビットであり、その基礎が2進数だ、とも言えるでしょう。
コンピュータ内部では全てのデータを「0」と「1」の２つの値だけで、つまり２進数で対応しています。その辺の具体的な内容を理解できればパソコン全般について、特にデータやファイルの値やサイズについて、その基礎部分が或る程度理解できるのではないでしょうか。

１０進数、２進数、８進数、１６進数

通常我々が使っている10進数は、0から9迄の10個の数字を使います。 これは手の指が10本有ることから自然に発達した数え方です。
10進数の桁をデジット（digit）と言いますが、これは、「指」と言う意味を持っています。

2進数字のことを「バイナリーデジット」と言います。
「バイナリー」とは「２進数の…」と言う意味です。2進数は、0と1の2つの数字だけを使い計算、表示します。 2進数の1桁はしたがって、0か1だけと言うことになります。 １の次は桁が繰り上がって10となります。 この場合（ジュウ）とは読みません。（イチマル、又はイチゼロ）と呼びます。これは後に出て来る8進数、16進数共通です。

コンピュータ での数の表現には、2進数の他16進数も使われます(8進数はあまり使われていないようです）。しかしそれはあくまでも表記の仕方であって、考え方、数え方は2進数です。
16進数表記は 文字コード、カラーコード、通信制御コード等、幅広く使われています。 2進数では桁が多くなり表示に適さない理由からです（後述）。

以下10進数、2進数、８進数、１６進数の対応表を掲載して置きます 。

10進数、2進数、8進数、16進数対応表
10進数 2進数 8進数 16進数 10進数 2進数 8進数 16進数
0 0 0 0 9 1001 11 9
1 1 1 1 10 1010 12 A
2 10 2 2 11 1011 13 B
3 11 3 3 12 1100 14 C
4 100 4 4 13 1101 15 D
5 101 5 5 14 1110 16 E
6 110 6 6 15 1111 17 F
7 111 7 7 16 10000 20 10
8 1000 10 8        

※ 日本と欧米での桁表示

ここで少し「位取り」と言うか、数値表示の単位（桁）について述べておきます。 パソコン関係では頻繁に出て来る言葉です。
日本式の位取りは、１から千までは一桁づつ、それ以上は、万、億、兆、京……、と４桁づつに括られています。
10000円を1万円、100000000円を1億円と書くことが有るように（10000万円と言わずに）……です。

昔（大昔）、日本ではコンマ（,）が４桁区切りで付けられていました。上記の日本式位取りを反映していた訳です。
でも今は３桁区切りで付いていますね。次に述べる欧米式の位取りに合わせたと言うことなんでしょうかね。

西欧では、或いはコンピュータでは３桁づつに括られて表示されます。
K（キロ）、M（メガ）、G（ギガ）、T（テラ）、Ｐ(ペタ）、E（エクサ）、Z（ゼタ）、Y（ヨタ）の様に。1,000Kで1M、1,000Mで1Gとなります。
同じように、少ない方にもミリ、マイクロ、ナノ、ピコ、フェムト、アト、ゼクト、ヨクト、という具合に 1,000分の1単位で小さくなって行きます。

ただ、パソコンでは2進数が使われているので、1,000とは言っても 通常使っている10進数の様に、丁度1,000にはならず実際には 1,024になります。1M（メガ）は1,000Kではなく1,024K になります。桁が小さいうちはどちらでもあまり問題が無いかも知れませんが、桁が大きくなった場合問題が出てきます。

1テラビットは何ビットになるか、皆さん考えてみて下さい。(1,024*1,024*1,024*1,024)

ビット

■ ビットとバイト

情報の最小単位は「二者択一」であり、この最小単位を「ビット」と呼びます。そしてこれを0と1の2つの数字で表します。 コンピュータの内部では、これを電圧のHi(High)とLo(Low)の２つの状態で対応しています。

※ このビットを最初に提唱したのは、「礼儀正しさと誠実さが伝説の域に入る（『不思議な量子』ーケネス・W・フォード著.日本評論社）」アメリカの偉大な物理学者ジョン・アーチボルト・ホイーラー（1911/7/9～2008/4/13)です。「 It from bit （それはビットから）」は彼の名言です。
ホイーラーは又、プランク尺度の提唱者であり、ブラックホール、ワームホール、量子の泡などの造語も彼に拠ります。

情報の最小単位

上記のようにビットは、0か1のどちらか（二者択一）です。これが2進数の1桁になります。つまり2進数の１桁をビットと言う訳です。バイナリーデジット(binary dijit）-2進数字の略です。
１桁は0か1のどちらか１つ、8ビットならば、0と1が8個並んだ状態を言います。

１０進数の桁をデジット（digit）と言います。
デジタルと言う言葉はこの形容詞で、「１０進数の」と言う意味も有るのですが、今は「数値で表される」と言う意味で使われています。

2進数の1桁・1ビットは、0か1だけの、どちらか1つです。
ここに情報を載せると、「無」「有」、「黒」「白」、「男」「女」、「敵」「味方」、「嫌い」「好き」、或いは「愛してない」「愛してる」等を表すことが出来ます。これはコンピュータに限らず、情報一般の最小単位です。

ビットと情報量

1ビットでは上記の様に、例えば「愛してる」「愛してない」等、情報の最小単位「二者択一」を表すことが出来ます。しかし、「どの程度」愛しているか、と言う情報は1ビットでは表現できません。

2桁(2ビット)では、00、　01、10、11　の4つのバリエーションが得られます。
「全然愛してない」、「3分の1愛している」、「3分の2愛している」、「全部愛してる」 この4つの表現が出来ます。 或いは「東西南北」 等に対応させる事が出来ます。

同じように、3ビットでは、8つ、4ビットでは16、5ビットで32、6ビットで64、 7ビットで128、8ビットで256、9ビットで512、10ビットで1024（＊注1）、になります。
要するに、2をビット数で階乗すればいいのです。

バイト

そして8ビット(=256)を一まとめにして、1バイトと言います。 コンピュータではバイト単位で情報のやり取りをしています。ビットではあまりに小さすぎて情報の単位として扱いにくいからです（＊注2）。
1バイト=8ビット＝256　と言う事になります。

あなたは、256通りの愛情表現が出来ますか？

この8ビットを一まとめにして1バイトとし、バイト単位でアドレスを付け、データ、コマンドすべてバイト単位で扱う、と言う考え方を最初に採用したのは、1964年発表されたIBMの360シリーズからだそうです。
なお、４ビットを1単位とする表現を「ニブル」と言うそうですが、使われているのを見たことが有りません。

（＊注1）上記「桁表示」で述べた、「2進数では、丁度1000、にならず1024になる」 と言ったことの意味です。
（＊注2）通信などではビット単位で表記されています（7.2Mbps 等）。

※ 「ビットは、0か1の2つのうちの一つ」と書きましたが、しかしもともと、0 は「無」であって、本来無いのです。「0 と言うもの」が有る訳ではないのです。 「有」つまり、1が発生して始めてその対立概念としての 0 が意識されるのですね。元々何も無いところには 0 も意識されません。
ですから、コンピュータでも、要するに「1」と言う信号を作ることだけ考えれば良いのです。1 が無いときは必然的に 0 になるのですから。

ビット長と16進数

ところで2進数表記について、ひとつ注意を要することが有ります。
１０進数では、1、2、3………10、11、12………100、101、102のように値が増えるごとに桁数も長くなって行きます。１億は100000000で９桁になりますね。
その点2進数では、表しているデータによって、桁数が決まっている、と言うことです。どう言うことかというと………、
1ビットの0は、0です。1は1です。
しかし同じ0でも8ビット（1バイト）の0は、00000000であり、1は00000001です。
24ビットの1は、00000000 00000000 00000001になります。

※ モノクロ1ビット画像の黒は0で、白は1が対応しています。
グレースケール8ビット画像の場合、00000000が黒、11111111が白。
フルカラー24ビット画像では、00000000 00000000 00000000が黒。
11111111 11111111 11111111が白になります。
表面的に同じ結果で有っても、データの種類によってビット長が違ってきます。 この辺の事情は後ほど詳述します。

※ 又、10進数の1は、「一つ」或いは「一番目」と言うような意味を持っていますが、2進数の1は、どちらかと言うと、「ビット長の中の一つ」と言う意味を 持っています。つまり1ビットの1は「二つの中の一つ、1/2」であり、1バイト（8ビット）の1は「1/256」です。
同じ 1 でも、データの重み、と言うことを考えれば当然 8ビットの方が重くなります。それだけデータサイズも大きくなる、と言うことです。

上記のように2進数は、値が増えるにつれビット（桁）が長くなり表示にも不具合が生じます。その為実際の表記では8進数や16進数が使われることになります。
16進数では2進数4ビットを1桁で表すことが出来ます（上記対応表参照）。
例えば、1バイトを構成する8ビットでは「11010001」のように、0と1が8個並んでいます。
これを16進数で表すと、D1と言うことになります。


コンピュータとビット

■ ビットとスイッチ

コンピュータはビットを電圧のLo(Low)、Hi(High)で表現します。つまりスイッチの「OFF」、「ON」処理で対応します。スイッチが切れて 電圧が掛かっていない状態を「0」、スイッチが繋がり電圧（5Ｖ）が掛かっている状態を「1」とします。

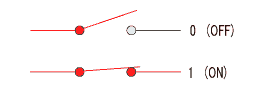2進数とビット　スイッチ1ビットはスイッチ1個で対応

1個のスイッチ（ビット）で表現できる情報は、0か1、2つのうちの1つです。
2進数の1桁、1ビットで表現できる情報は、ON、OFF等、極めて単純なものです。又10進数に比べ桁数が多くなり、一見効率が悪そうです。
こんな「出来の悪い」2進数を、何故コンピュータが使うのでしょう。

ビットは単純、しかし組み合わせると………。

1ビットは、0、1, コンピュータ内では電気信号のOFF、ONで対応出来る極めて単純な情報セットです。 しかし上記の「愛情表現」の例で見られるように、ビットセットを組み合わせることにより、表現できる情報量は飛躍的に（階乗的に）高まります。
その際でも、単位となるビットセット（パソコンでの回路）はあくまでも、0、1（OFF、ON）の単純なままで良いのです。このことを少し具体的に見てみましょう。

ビットのパラレル（並列）処理

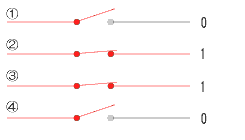ビットスイッチ　パラレル右図 を見て下さい。
スイッチ回路が4個、並列に並んでいます。これは其のまま4ビットを表しています。 各スイッチ（1ビット）毎に、OFF、ON（0,1）を表現できます。
スイッチが繋がっていれば電流が流れ、ON（1）になり、切れていれば電量は流れず、OFF（0）になります。
この場合（4ビット）、表せる情報バリエーションは、2の4乗，つまり16になります。
そしてこのスイッチの数を増やす毎に、情報バリエーションは飛躍的に増加します。

※ 32ビットパソコン

従来パソコンの主流は、32ビットCPUでした。今後発売になるパソコンは殆ど64ビットになっています。
ここでは32ビットで考えてみます。つまり上図のスイッチが並列に32個並んでいて、一度に32ビットの処理 が出来るのですが、それで表現できる情報バリエーションは、2の32乗、実に4,294,967,296、およそ43億と言う膨大な数になります（64ビットではいくつになるか？、到底電卓の桁数が足りません）。
その場合でも、個々の要素（素子）としては、あくまでも極めて単純なON,OFF回路に過ぎません。

電気信号が切れているか、通っているか、だけが認識出来れば良いので有って、電圧の変化等、量的な「ぶれ」 に影響される事が有りません。要するにノイズが入りにくく、信頼性が高いのです。 処理が単純だと言う事は当然システムの単純化、コストの低減に繋がります。
若し１０進数を使い、それに対応した10種類の処理を使い分けなければならないとしたら、ハードもそれを制御するソフトも、今と比較にならない位複雑で高価で、しかもエラー多発のシステムになっていたでしょう。

※ ビットのシリアル（直列）処理

なおこれはあくまでもスイッチがパラレル（並列）に並んでいる状況での話です。シリアル（直列）配置では幾ら多くのスイッチが並んでいても1ビットの表現しか出来ません。

ビットスイッチ　シリアル右図はパラレル配置の図と同じスイッチ状態ですが、配列がシリアル（直列）になっています。
この場合、スイッチが全て繋がっていれば電流が流れ、1、 一個でも繋がっていないスイッチが有れば電流は流れず、 0、となります。
つまりシリアルでは、幾らスイッチ数が多くても、結局1ビットの効果しか得られません。

CPUのビット処理とバス（bus）

32ビットCPUは上記のように、一度に約43億のON、OFF処理を行っています。しかも最近のパソコン処理能力は、クロック周波数3ギガHz (10/３/10現在）を超えています。つまり約43億の処理を一秒間に30億回やってのけていることになります。
しかし同時に、CPUがいくら高速なパラレル処理をこなしても、その信号を伝達する伝送経路がそれに対応していなければなりません。

CPUやメモリの現物、或いは写真を見た人は、ムカデの足のようなもの、或いは生け花に使う剣山の針のようなものがいっぱい付いているのに気が付いたと思います。あの針の1本1本は、CPUの32のビットスイッチに対応しているのです。
又、パソコンの蓋を開けて中を見た人は、帯の様に幅広い電気コードでデバイス同士がが繋がっているのに気が付いたと思います。
実は、マザーボードにはCPUやメモリを繋ぐ一番広い信号の通り道があります。コンピュータの信号の通り道を「バス（bus）」と言いますが1ビットに対応した一本一本の電線が幅広く並んでいるのです。 つまりCPUやメモリだけでなく、伝送経路もパラレルでビットに対応している訳です。
バスは接続されているデバイスによってその伝送経路の数が違います。これを「バス幅」と言います。一番メインとなるデータバスは64本、つまり64ビットのバス幅を持っています。

■ その他2進数を使う理由あれこれ

その他2進数を使うことの、メリットだと思われる理由を若干挙げて見ましょう。

実は２進数は効率が良い

  1. １０進数の「256」 を２進数で記述すると「100000000」になります。この二つの数字をコンピュータ が認識する手順を考えて見ましょう。

  2. ２進数の方は0か1かを判別するだけで良いから、、各桁ごとに2回の照合で良い。それを9桁分だから合計18回の照合作業を必要とする。
    １０進数では各桁、0から9迄、10回の照合を必要とし、3桁だから合計30回の照合作業を必要とする

同じ情報量なら、素子数を少なく出来る

手の指を使い、１０進数と２進数の情報量を比べて見ましょう(※指を使った２進数表現)。

  1. 右手を出し、手のひらを自分に向けます。

  2. 指を折った状態を0、立てた状態を1とします。
    手を握った状態（全ての指を折った状態）では0、 親指だけ立てた状態は1、人差し指だけを立てた状態は10 となります。

  3. 5本の指全部を立てた状態は11111になり、１０進数表現では31になります。
    つまり片手で、0を含め32通りの数を数えられることになります。

※ １０進数で偶数（２進数で桁上がりの時）、必ず親指が折れています。

１０進数の桁を片手で表現することは困難で、通常 手を握った（指を使わない）状態（つまり０）を含め、片手で１０進数の６個の数を表現できます。

２進数表現では、各指にビット（２進数の桁、左記Column参照）を割り当てれば５ビット（5本の指）の表現が出来、0～31迄の表現が出来ます。
指を半導体素子数と考えれば、同じ情報量を少ない素子数で表せることが理解できると思います